gptools: Gaussian processes with arbitrary derivative constraints and predictions¶
Source home: https://github.com/markchil/gptools
Releases: https://pypi.python.org/pypi/gptools/
Installation is as simple as:
pip install gptools
A comprehensive demo is provided at https://github.com/markchil/gptools/blob/master/demo/demo.py, with extensive comments showing how the code functions on real data (also hosted on the github). This should be consulted in parallel with this manual.
Overview¶
gptools is a Python package that provides a convenient, powerful and extensible implementation of Gaussian process regression (GPR). Central to gptools‘ implementation is support for derivatives and their variances. Furthermore, the implementation supports the incorporation of arbitrary linearly transformed quantities into the GP.
There are two key classes:
GaussianProcessis the main class to represent a GP.Kernel(and its many subclasses) represents a covariance kernel, and must be provided when constructing aGaussianProcess. Separate kernels to describe the underlying signal and the noise are supported.
A third class, JointPrior, allows you to construct a hyperprior of arbitrary complexity to dictate how the hyperparameters are handled.
Creating a Gaussian process is as simple as:
import gptools
k = gptools.SquaredExponentialKernel()
gp = gptools.GaussianProcess(k)
But, the default bounds on the hyperparameters are very wide and can cause the optimizer/MCMC sampler to fail. So, it is usually a better idea to define the covariance kernel as:
k = gptools.SquaredExponentialKernel(param_bounds=[(0, 1e3), (0, 100)])
You will have to pick appropriate numbers by inspecting the typical range of your data.
Furthermore, you can include an explicit mean function by passing
the appropriate MeanFunction instance into the mu keyword:
gp = gptools.GaussianProcess(k, mu=gptools.LinearMeanFunction())
This will enable you to perform inference (both empirical and full Bayes) for
the hyperparameters of the mean function. Essentially, gptools can
perform nonlinear Bayesian regression with a Gaussian process fit to the
residuals.
You then add the training data using the add_data() method:
gp.add_data(x, y, err_y=stddev_y)
Here, err_y is the 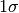 uncertainty on the observations y. For exact values, simply omit this keyword. Adding a derivative observation is as simple as specifying the derivative order with the n keyword:
uncertainty on the observations y. For exact values, simply omit this keyword. Adding a derivative observation is as simple as specifying the derivative order with the n keyword:
gp.add_data(0, 0, n=1)
This will force the slope at 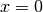 to be exactly zero. Quantities that represent an arbitrary linear transformation of the “basic” observations can be added by specifying the T keyword:
to be exactly zero. Quantities that represent an arbitrary linear transformation of the “basic” observations can be added by specifying the T keyword:
gp.add_data(x, y, T=T)
This will add the value(s) 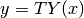 to the training data, where here
to the training data, where here 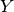 represents the “basic” (untransformed) observations and
represents the “basic” (untransformed) observations and 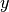 represents the transformed observations. This also supports the err_y and n keywords. Here, err_y is the error on the transformed quantity
represents the transformed observations. This also supports the err_y and n keywords. Here, err_y is the error on the transformed quantity 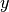 . n applies to the latent variables
. n applies to the latent variables 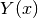 .
.
Once the GP has been populated with training data, there are two approaches supported to handle the hyperparameters.
The simplest approach is to use an empirical Bayes approach and compute the maximum a posteriori (MAP) estimate. This is accomplished using the optimize_hyperparameters() method of the GaussianProcess instance:
gp.optimize_hyperparameters()
This will randomly start the optimizer at points distributed according to the hyperprior several times in order to ensure that the global maximum is obtained. If you have a machine with multiple cores, these random starts will be performed in parallel. You can set the number of starts using the random_starts keyword, and you can set the number of processes used using the num_proc keyword.
For a more complete accounting of the uncertainties in the model, you can choose to use a fully Bayesian approach by using Markov chain Monte Carlo (MCMC) techniques to produce samples of the hyperposterior. The samples are produced directly with sample_hyperparameter_posterior(), though it will typically be more convenient to simply call predict() with the use_MCMC keyword set to True.
In order to make predictions, use the predict() method:
y_star, err_y_star = gp.predict(x_star)
By default, the mean and standard deviation of the GP posterior are returned. To compute only the mean and save some time, set the return_std keyword to False. To make predictions of derivatives, set the n keyword. To make a prediction of a linearly transformed quantity, set the output_transform keyword.
For a convenient wrapper for applying gptools to multivariate data, see profiletools at https://github.com/markchil/profiletools
Kernels¶
A number of kernels are provided to allow many types of data to be fit:
DiagonalNoiseKernelimplements homoscedastic noise. The noise is tied to a specific derivative order. This allows you to, for instance, have noise on your observations but have noiseless derivative constraints, or to have different noise levels for observations and derivatives. Note that you can also specify potentially heteroscedastic noise explicitly when adding data to the process.SquaredExponentialKernelimplements the SE kernel which is infinitely differentiable.MaternKernelimplements the entire Matern class of covariance functions, which are characterized by a hyperparameter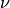 . A process having the Matern kernel is only mean-square differentiable for derivative order
. A process having the Matern kernel is only mean-square differentiable for derivative order 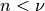 . Note that this class does not support arbitrary derivatives at this point. If you need this feature, try using
. Note that this class does not support arbitrary derivatives at this point. If you need this feature, try using MaternKernelArb, but note that this is very slow!Matern52Kernelimplements a specialized Matern kernel with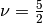 which efficiently supports 0th and 1st derivatives.
which efficiently supports 0th and 1st derivatives.RationalQuadraticKernelimplements the rational quadratic kernel, which is a scale mixture over SE kernels.GibbsKernel1dand its subclasses implements the Gibbs kernel, which is a nonstationary form of the SE kernel.MaskedKernelcreates a kernel that only operates on a subset of dimensions. Use this along with the sum and product operations to create kernels that encode different properties in different dimensions.ArbitraryKernelcreates a kernel with an arbitrary covariance function and computes the derivatives as needed usingmpmathto perform numerical differentiation. Naturally, this is very slow but is useful to let you explore the properties of arbitrary kernels without having to write a complete implementation.
In most cases, these kernels have been constructed in a way to allow inputs of arbitrary dimension. Each dimension has a length scale hyperparameter that can be separately optimized over or held fixed. Arbitrary derivatives with respect to each dimension can be taken, including computation of the covariance for those observations.
Other kernels can be implemented by extending the Kernel class. Furthermore, kernels may be added or multiplied together to yield a new, valid kernel.
Notes¶
gptools has been developed and tested on Python 2.7 and scipy 0.14.0. It may work just as well on other versions, but has not been tested.
If you find this software useful, please be sure to cite it:
M.A. Chilenski et al. 2015 Nucl. Fusion 55 023012