gptools.kernel package¶
Submodules¶
gptools.kernel.core module¶
Core kernel classes: contains the base Kernel class and helper subclasses.
-
class
gptools.kernel.core.Kernel(num_dim=1, num_params=0, initial_params=None, fixed_params=None, param_bounds=None, param_names=None, enforce_bounds=False, hyperprior=None)[source]¶ Bases:
objectCovariance kernel base class. Not meant to be explicitly instantiated!
Initialize the kernel with the given number of input dimensions.
When implementing an isotropic covariance kernel, the covariance length scales should be the last num_dim elements in params.
Parameters: num_dim : positive int
Number of dimensions of the input data. Must be consistent with the X and Xstar values passed to the
GaussianProcessyou wish to use the covariance kernel with. Default is 1.num_params : Non-negative int
Number of parameters in the model.
initial_params :
Arrayor other Array-like, (num_params,), optionalInitial values to set for the hyperparameters. Default is None, in which case 1 is used for the initial values.
fixed_params :
Arrayor other Array-like of bool, (num_params,), optionalSets which hyperparameters are considered fixed when optimizing the log likelihood. A True entry corresponds to that element being fixed (where the element ordering is as defined in the class). Default value is None (no hyperparameters are fixed).
param_bounds : list of 2-tuples (num_params,), optional
List of bounds for each of the hyperparameters. Each 2-tuple is of the form (lower, upper). If there is no bound in a given direction, it works best to set it to something big like 1e16. Default is (0.0, 1e16) for each hyperparameter. Note that this is overridden by the hyperprior keyword, if present.
param_names : list of str (num_params,), optional
List of labels for the hyperparameters. Default is all empty strings.
enforce_bounds : bool, optional
If True, an attempt to set a hyperparameter outside of its bounds will result in the hyperparameter being set right at its bound. If False, bounds are not enforced inside the kernel. Default is False (do not enforce bounds).
hyperprior :
JointPriorinstance or list, optionalJoint prior distribution for all hyperparameters. Can either be given as a
JointPriorinstance or a list of num_params callables or py:class:rv_frozen instances fromscipy.stats, in which case aIndependentJointPrioris constructed with these as the independent priors on each hyperparameter. Default is a uniform PDF on all hyperparameters.Raises: ValueError
If num_dim is not a positive integer or the lengths of the input vectors are inconsistent.
GPArgumentError
if fixed_params is passed but initial_params is not.
Attributes
num_free_paramsReturns the number of free parameters. free_param_idxsReturns the indices of the free parameters in the main arrays of parameters, etc. free_paramsReturns the values of the free hyperparameters. free_param_boundsReturns the bounds of the free hyperparameters. free_param_namesReturns the names of the free hyperparameters. num_params (int) Number of parameters. num_dim (int) Number of dimensions. param_names (list of str, (num_params,)) List of the labels for the hyperparameters. enforce_bounds (bool) If True, do not allow hyperparameters to be set outside of their bounds. params ( Arrayof float, (num_params,)) Array of parameters.fixed_params ( Arrayof bool, (num_params,)) Array of booleans indicated which parameters inparamsare fixed.hyperprior ( JointPriorinstance) Joint prior distribution for the hyperparameters.param_bounds ( CombinedBounds) The bounds on the hyperparameters. Actually a getter method with a property decorator.-
param_bounds¶
-
__call__(Xi, Xj, ni, nj, hyper_deriv=None, symmetric=False)[source]¶ Evaluate the covariance between points Xi and Xj with derivative order ni, nj.
Note that this method only returns the covariance – the hyperpriors and potentials stored in this kernel must be applied separately.
Parameters: Xi :
Matrixor other Array-like, (M, D)M inputs with dimension D.
Xj :
Matrixor other Array-like, (M, D)M inputs with dimension D.
ni :
Matrixor other Array-like, (M, D)M derivative orders for set i.
nj :
Matrixor other Array-like, (M, D)M derivative orders for set j.
hyper_deriv : Non-negative int or None, optional
The index of the hyperparameter to compute the first derivative with respect to. If None, no derivatives are taken. Default is None (no hyperparameter derivatives).
symmetric : bool, optional
Whether or not the input Xi, Xj are from a symmetric matrix. Default is False.
Returns: Kij :
Array, (M,)Covariances for each of the M Xi, Xj pairs.
Notes
THIS IS ONLY A METHOD STUB TO DEFINE THE NEEDED CALLING FINGERPRINT!
-
set_hyperparams(new_params)[source]¶ Sets the free hyperparameters to the new parameter values in new_params.
Parameters: new_params :
Arrayor other Array-like, (len(self.free_params),)New parameter values, ordered as dictated by the docstring for the class.
-
num_free_params¶ Returns the number of free parameters.
-
free_param_idxs¶ Returns the indices of the free parameters in the main arrays of parameters, etc.
-
free_params¶ Returns the values of the free hyperparameters.
Returns: free_params :
ArrayArray of the free parameters, in order.
-
free_param_bounds¶ Returns the bounds of the free hyperparameters.
Returns: free_param_bounds :
ArrayArray of the bounds of the free parameters, in order.
-
free_param_names¶ Returns the names of the free hyperparameters.
Returns: free_param_names :
ArrayArray of the names of the free parameters, in order.
-
__add__(other)[source]¶ Add two Kernels together.
Parameters: other :
KernelKernel to be added to this one.
Returns: sum :
SumKernelInstance representing the sum of the two kernels.
-
__mul__(other)[source]¶ Multiply two Kernels together.
Parameters: other :
KernelKernel to be multiplied by this one.
Returns: prod :
ProductKernelInstance representing the product of the two kernels.
-
-
class
gptools.kernel.core.BinaryKernel(k1, k2)[source]¶ Bases:
gptools.kernel.core.KernelAbstract class for binary operations on kernels (addition, multiplication, etc.).
Parameters: k1, k2 : Kernelinstances to be combinedNotes
k1 and k2 must have the same number of dimensions.
-
enforce_bounds¶ Boolean indicating whether or not the kernel will explicitly enforce the bounds defined by the hyperprior.
-
fixed_params¶
-
free_param_bounds¶ Returns the bounds of the free hyperparameters.
Returns: free_param_bounds :
ArrayArray of the bounds of the free parameters, in order.
-
free_param_names¶ Returns the names of the free hyperparameters.
Returns: free_param_names :
ArrayArray of the names of the free parameters, in order.
-
params¶
-
-
class
gptools.kernel.core.SumKernel(k1, k2)[source]¶ Bases:
gptools.kernel.core.BinaryKernelThe sum of two kernels.
-
__call__(*args, **kwargs)[source]¶ Evaluate the covariance between points Xi and Xj with derivative order ni, nj.
Parameters: Xi :
Matrixor other Array-like, (M, D)M inputs with dimension D.
Xj :
Matrixor other Array-like, (M, D)M inputs with dimension D.
ni :
Matrixor other Array-like, (M, D)M derivative orders for set i.
nj :
Matrixor other Array-like, (M, D)M derivative orders for set j.
symmetric : bool, optional
Whether or not the input Xi, Xj are from a symmetric matrix. Default is False.
Returns: Kij :
Array, (M,)Covariances for each of the M Xi, Xj pairs.
-
-
class
gptools.kernel.core.ProductKernel(k1, k2)[source]¶ Bases:
gptools.kernel.core.BinaryKernelThe product of two kernels.
-
__call__(Xi, Xj, ni, nj, **kwargs)[source]¶ Evaluate the covariance between points Xi and Xj with derivative order ni, nj.
Parameters: Xi :
Matrixor other Array-like, (M, D)M inputs with dimension D.
Xj :
Matrixor other Array-like, (M, D)M inputs with dimension D.
ni :
Matrixor other Array-like, (M, D)M derivative orders for set i.
nj :
Matrixor other Array-like, (M, D)M derivative orders for set j.
symmetric : bool, optional
Whether or not the input Xi, Xj are from a symmetric matrix. Default is False.
Returns: Kij :
Array, (M,)Covariances for each of the M Xi, Xj pairs.
Raises: NotImplementedError
If the hyper_deriv keyword is given and is not None.
-
-
class
gptools.kernel.core.ChainRuleKernel(num_dim=1, num_params=0, initial_params=None, fixed_params=None, param_bounds=None, param_names=None, enforce_bounds=False, hyperprior=None)[source]¶ Bases:
gptools.kernel.core.KernelAbstract class for the common methods in creating kernels that require application of Faa di Bruno’s formula.
Implementing classes should provide the following methods:
- _compute_k(self, tau): Should return the value of k(tau) at the given values of tau, but without multiplying by sigma_f. This is done separately for efficiency.
- _compute_y(self, tau, return_r2l2=False): Should return the “inner form” y(tau) to use with Faa di Bruno’s formula. If return_r2l2 is True, should also return the r2l2 matrix from self._compute_r2l2(tau).
- _compute_dk_dy(self, y, n): Should compute the n`th derivative of the kernel `k with respect to y at the locations y.
- _compute_dy_dtau(self, tau, b, r2l2): Should compute the derivatives of y with respect to the elements of tau as indicated in b.
-
__call__(Xi, Xj, ni, nj, hyper_deriv=None, symmetric=False)[source]¶ Evaluate the covariance between points Xi and Xj with derivative order ni, nj.
Parameters: Xi :
Matrixor other Array-like, (M, D)M inputs with dimension D.
Xj :
Matrixor other Array-like, (M, D)M inputs with dimension D.
ni :
Matrixor other Array-like, (M, D)M derivative orders for set i.
nj :
Matrixor other Array-like, (M, D)M derivative orders for set j.
hyper_deriv : Non-negative int or None, optional
The index of the hyperparameter to compute the first derivative with respect to. If None, no derivatives are taken. Hyperparameter derivatives are not supported at this point. Default is None.
symmetric : bool
Whether or not the input Xi, Xj are from a symmetric matrix. Default is False.
Returns: Kij :
Array, (M,)Covariances for each of the M Xi, Xj pairs.
Raises: NotImplementedError
If the hyper_deriv keyword is not None.
-
class
gptools.kernel.core.ArbitraryKernel(cov_func, num_dim=1, num_proc=0, num_params=None, **kwargs)[source]¶ Bases:
gptools.kernel.core.KernelCovariance kernel from an arbitrary covariance function.
Computes derivatives using
mpmath.diff()and is hence in general much slower than a hard-coded implementation of a given kernel.Parameters: num_dim : positive int
Number of dimensions of the input data. Must be consistent with the X and Xstar values passed to the
GaussianProcessyou wish to use the covariance kernel with.cov_func : callable, takes >= 2 args
Covariance function. Must take arrays of Xi and Xj as the first two arguments. The subsequent (scalar) arguments are the hyperparameters. The number of parameters is found by inspection of cov_func itself, or with the num_params keyword.
num_proc : int or None, optional
Number of procs to use in evaluating covariance derivatives. 0 means to do it in serial, None means to use all available cores. Default is 0 (serial evaluation).
num_params : int or None, optional
Number of hyperparameters. If None, inspection will be used to infer the number of hyperparameters (but will fail if you used clever business with *args, etc.). Default is None (use inspection to find argument count).
**kwargs
All other keyword parameters are passed to
Kernel.Attributes
cov_func (callable) The covariance function num_proc (non-negative int) Number of processors to use in evaluating covariance derivatives. 0 means serial. -
__call__(Xi, Xj, ni, nj, hyper_deriv=None, symmetric=False)[source]¶ Evaluate the covariance between points Xi and Xj with derivative order ni, nj.
Parameters: Xi :
Matrixor other Array-like, (M, D)M inputs with dimension D.
Xj :
Matrixor other Array-like, (M, D)M inputs with dimension D.
ni :
Matrixor other Array-like, (M, D)M derivative orders for set i.
nj :
Matrixor other Array-like, (M, D)M derivative orders for set j.
hyper_deriv : Non-negative int or None, optional
The index of the hyperparameter to compute the first derivative with respect to. If None, no derivatives are taken. Hyperparameter derivatives are not supported at this point. Default is None.
symmetric : bool, optional
Whether or not the input Xi, Xj are from a symmetric matrix. Default is False.
Returns: Kij :
Array, (M,)Covariances for each of the M Xi, Xj pairs.
Raises: NotImplementedError
If the hyper_deriv keyword is not None.
-
-
class
gptools.kernel.core.MaskedKernel(base, total_dim=2, mask=[0], scale=None)[source]¶ Bases:
gptools.kernel.core.KernelCreates a kernel that is only masked to operate on certain dimensions, or has scaling/shifting.
This can be used, for instance, to put a squared exponential kernel in one direction and a Matern kernel in the other.
Overrides
__getattribute__()and__setattr__()to make all setting/accessing go to the base kernel.Parameters: base :
KernelinstanceThe
Kernelto apply in the dimensions specified in mask.total_dim : int, optional
The total number of dimensions the masked kernel should have. Default is 2.
mask : list or other array-like, optional
1d list of indices of dimensions X to include when passing to the base kernel. Length must be base.num_dim. Default is [0] (i.e., just pass the first column of X to a univariate base kernel).
scale : list or other array-like, optional
1d list of scale factors to apply to the elements in Xi, Xj. Default is ones. Length must be equal to 2`base.num_dim`.
-
__getattribute__(name)[source]¶ Gets all attributes from the base kernel.
The exceptions are ‘base’, ‘mask’, ‘maskC’, ‘num_dim’, ‘scale’ and any special method (i.e., a method/attribute having leading and trailing double underscores), which are taken from
MaskedKernel.
-
__setattr__(name, value)[source]¶ Sets all attributes in the base kernel.
The exceptions are ‘base’, ‘mask’, ‘maskC’, ‘num_dim’, ‘scale’ and any special method (i.e., a method/attribute having leading and trailing double underscores), which are set in
MaskedKernel.
-
__call__(Xi, Xj, ni, nj, **kwargs)[source]¶ Evaluate the covariance between points Xi and Xj with derivative order ni, nj.
Note that in the argument specifications, D is the total_dim specified in the constructor (i.e.,
num_dimfor theMaskedKernelinstance itself).Parameters: Xi :
Matrixor other Array-like, (M, D)M inputs with dimension D.
Xj :
Matrixor other Array-like, (M, D)M inputs with dimension D.
ni :
Matrixor other Array-like, (M, D)M derivative orders for set i.
nj :
Matrixor other Array-like, (M, D)M derivative orders for set j.
hyper_deriv : Non-negative int or None, optional
The index of the hyperparameter to compute the first derivative with respect to. If None, no derivatives are taken. Default is None (no hyperparameter derivatives).
symmetric : bool, optional
Whether or not the input Xi, Xj are from a symmetric matrix. Default is False.
Returns: Kij :
Array, (M,)Covariances for each of the M Xi, Xj pairs.
-
gptools.kernel.gibbs module¶
Provides classes and functions for creating SE kernels with warped length scales.
-
gptools.kernel.gibbs.tanh_warp_arb(X, l1, l2, lw, x0)[source]¶ Warps the X coordinate with the tanh model
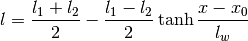
Parameters: X :
Array, (M,) or scalar floatM locations to evaluate length scale at.
l1 : positive float
Small-X saturation value of the length scale.
l2 : positive float
Large-X saturation value of the length scale.
lw : positive float
Length scale of the transition between the two length scales.
x0 : float
Location of the center of the transition between the two length scales.
Returns: l :
Array, (M,) or scalar floatThe value of the length scale at the specified point.
-
gptools.kernel.gibbs.gauss_warp_arb(X, l1, l2, lw, x0)[source]¶ Warps the X coordinate with a Gaussian-shaped divot.
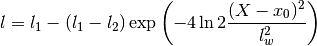
Parameters: X :
Array, (M,) or scalar floatM locations to evaluate length scale at.
l1 : positive float
Global value of the length scale.
l2 : positive float
Pedestal value of the length scale.
lw : positive float
Width of the dip.
x0 : float
Location of the center of the dip in length scale.
Returns: l :
Array, (M,) or scalar floatThe value of the length scale at the specified point.
-
class
gptools.kernel.gibbs.GibbsFunction1dArb(warp_function)[source]¶ Bases:
objectWrapper class for the Gibbs covariance function, permits the use of arbitrary warping.
The covariance function is given by
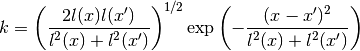
Parameters: warp_function : callable
The function that warps the length scale as a function of X. Must have the fingerprint (Xi, l1, l2, lw, x0).
-
__call__(Xi, Xj, sigmaf, l1, l2, lw, x0)[source]¶ Evaluate the covariance function between points Xi and Xj.
Parameters: Xi, Xj :
Array,mpfor scalar floatPoints to evaluate covariance between. If they are
Array,scipyfunctions are used, otherwisempmathfunctions are used.sigmaf : scalar float
Prefactor on covariance.
l1, l2, lw, x0 : scalar floats
Parameters of length scale warping function, passed to
warp_function.Returns: k :
ArrayormpfCovariance between the given points.
-
-
class
gptools.kernel.gibbs.GibbsKernel1dTanhArb(**kwargs)[source]¶ Bases:
gptools.kernel.core.ArbitraryKernelGibbs warped squared exponential covariance function in 1d.
Computes derivatives using
mpmath.diff()and is hence in general much slower than a hard-coded implementation of a given kernel.The covariance function is given by
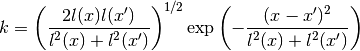
Warps the length scale using a hyperbolic tangent:
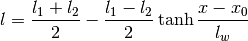
The order of the hyperparameters is:
0 sigmaf Amplitude of the covariance function 1 l1 Small-X saturation value of the length scale. 2 l2 Large-X saturation value of the length scale. 3 lw Length scale of the transition between the two length scales. 4 x0 Location of the center of the transition between the two length scales. Parameters: **kwargs
All parameters are passed to
Kernel.
-
class
gptools.kernel.gibbs.GibbsKernel1dGaussArb(**kwargs)[source]¶ Bases:
gptools.kernel.core.ArbitraryKernelGibbs warped squared exponential covariance function in 1d.
Computes derivatives using
mpmath.diff()and is hence in general much slower than a hard-coded implementation of a given kernel.The covariance function is given by
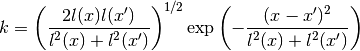
Warps the length scale using a gaussian:
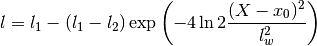
The order of the hyperparameters is:
0 sigmaf Amplitude of the covariance function 1 l1 Global value of the length scale. 2 l2 Pedestal value of the length scale. 3 lw Width of the dip. 4 x0 Location of the center of the dip in length scale. Parameters: **kwargs
All parameters are passed to
Kernel.
-
class
gptools.kernel.gibbs.GibbsKernel1d(l_func, num_params=None, **kwargs)[source]¶ Bases:
gptools.kernel.core.KernelUnivariate Gibbs kernel with arbitrary length scale warping for low derivatives.
The covariance function is given by
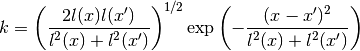
The derivatives are hard-coded using expressions obtained from Mathematica.
Parameters: l_func : callable
Function that dictates the length scale warping and its derivative. Must have fingerprint (x, n, p1, p2, ...) where p1 is element one of the kernel’s parameters (i.e., element zero is skipped).
num_params : int, optional
The number of parameters of the length scale function. If not passed, introspection will be used to determine this. This will fail if you have used the *args syntax in your function definition. This count should include sigma_f, even though it is not passed to the length scale function.
**kwargs
All remaining arguments are passed to
Kernel.-
__call__(Xi, Xj, ni, nj, hyper_deriv=None, symmetric=False)[source]¶ Evaluate the covariance between points Xi and Xj with derivative order ni, nj.
Parameters: Xi :
Matrixor other Array-like, (M, D)M inputs with dimension D.
Xj :
Matrixor other Array-like, (M, D)M inputs with dimension D.
ni :
Matrixor other Array-like, (M, D)M derivative orders for set i.
nj :
Matrixor other Array-like, (M, D)M derivative orders for set j.
hyper_deriv : Non-negative int or None, optional
The index of the hyperparameter to compute the first derivative with respect to. If None, no derivatives are taken. Hyperparameter derivatives are not supported at this point. Default is None.
symmetric : bool, optional
Whether or not the input Xi, Xj are from a symmetric matrix. Default is False.
Returns: Kij :
Array, (M,)Covariances for each of the M Xi, Xj pairs.
Raises: NotImplementedError
If the hyper_deriv keyword is not None.
-
-
gptools.kernel.gibbs.tanh_warp(x, n, l1, l2, lw, x0)[source]¶ Implements a tanh warping function and its derivative.
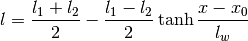
Parameters: x : float or array of float
Locations to evaluate the function at.
n : int
Derivative order to take. Used for ALL of the points.
l1 : positive float
Left saturation value.
l2 : positive float
Right saturation value.
lw : positive float
Transition width.
x0 : float
Transition location.
Returns: l : float or array
Warped length scale at the given locations.
Raises: NotImplementedError
If n > 1.
-
class
gptools.kernel.gibbs.GibbsKernel1dTanh(**kwargs)[source]¶ Bases:
gptools.kernel.gibbs.GibbsKernel1dGibbs warped squared exponential covariance function in 1d.
Uses hard-coded implementation up to first derivatives.
The covariance function is given by
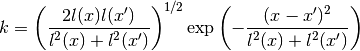
Warps the length scale using a hyperbolic tangent:
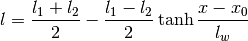
The order of the hyperparameters is:
0 sigmaf Amplitude of the covariance function 1 l1 Small-X saturation value of the length scale. 2 l2 Large-X saturation value of the length scale. 3 lw Length scale of the transition between the two length scales. 4 x0 Location of the center of the transition between the two length scales. Parameters: **kwargs
All parameters are passed to
Kernel.
-
gptools.kernel.gibbs.double_tanh_warp(x, n, lcore, lmid, ledge, la, lb, xa, xb)[source]¶ Implements a sum-of-tanh warping function and its derivative.
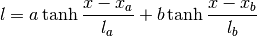
Parameters: x : float or array of float
Locations to evaluate the function at.
n : int
Derivative order to take. Used for ALL of the points.
lcore : float
Core length scale.
lmid : float
Intermediate length scale.
ledge : float
Edge length scale.
la : positive float
Transition of first tanh.
lb : positive float
Transition of second tanh.
xa : float
Transition of first tanh.
xb : float
Transition of second tanh.
Returns: l : float or array
Warped length scale at the given locations.
Raises: NotImplementedError
If n > 1.
-
class
gptools.kernel.gibbs.GibbsKernel1dDoubleTanh(**kwargs)[source]¶ Bases:
gptools.kernel.gibbs.GibbsKernel1dGibbs warped squared exponential covariance function in 1d.
Uses hard-coded implementation up to first derivatives.
The covariance function is given by
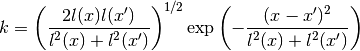
Warps the length scale using two hyperbolic tangents:
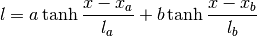
The order of the hyperparameters is:
0 sigmaf Amplitude of the covariance function 1 lcore Core length scale 2 lmid Intermediate length scale 3 ledge Edge length scale 4 la Width of first tanh 5 lb Width of second tanh 6 xa Center of first tanh 7 xb Center of second tanh Parameters: **kwargs
All parameters are passed to
Kernel.
-
gptools.kernel.gibbs.cubic_bucket_warp(x, n, l1, l2, l3, x0, w1, w2, w3)[source]¶ Warps the length scale with a piecewise cubic “bucket” shape.
Parameters: x : float or array-like of float
Locations to evaluate length scale at.
n : non-negative int
Derivative order to evaluate. Only first derivatives are supported.
l1 : positive float
Length scale to the left of the bucket.
l2 : positive float
Length scale in the bucket.
l3 : positive float
Length scale to the right of the bucket.
x0 : float
Location of the center of the bucket.
w1 : positive float
Width of the left side cubic section.
w2 : positive float
Width of the bucket.
w3 : positive float
Width of the right side cubic section.
-
class
gptools.kernel.gibbs.GibbsKernel1dCubicBucket(**kwargs)[source]¶ Bases:
gptools.kernel.gibbs.GibbsKernel1dGibbs warped squared exponential covariance function in 1d.
Uses hard-coded implementation up to first derivatives.
The covariance function is given by
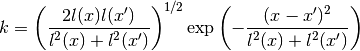
Warps the length scale using a “bucket” function with cubic joins.
The order of the hyperparameters is:
0 sigmaf Amplitude of the covariance function 1 l1 Length scale to the left of the bucket. 2 l2 Length scale in the bucket. 3 l3 Length scale to the right of the bucket. 4 x0 Location of the center of the bucket. 5 w1 Width of the left side cubic section. 6 w2 Width of the bucket. 7 w3 Width of the right side cubic section. Parameters: **kwargs
All parameters are passed to
Kernel.
-
gptools.kernel.gibbs.quintic_bucket_warp(x, n, l1, l2, l3, x0, w1, w2, w3)[source]¶ Warps the length scale with a piecewise quintic “bucket” shape.
Parameters: x : float or array-like of float
Locations to evaluate length scale at.
n : non-negative int
Derivative order to evaluate. Only first derivatives are supported.
l1 : positive float
Length scale to the left of the bucket.
l2 : positive float
Length scale in the bucket.
l3 : positive float
Length scale to the right of the bucket.
x0 : float
Location of the center of the bucket.
w1 : positive float
Width of the left side quintic section.
w2 : positive float
Width of the bucket.
w3 : positive float
Width of the right side quintic section.
-
class
gptools.kernel.gibbs.GibbsKernel1dQuinticBucket(**kwargs)[source]¶ Bases:
gptools.kernel.gibbs.GibbsKernel1dGibbs warped squared exponential covariance function in 1d.
Uses hard-coded implementation up to first derivatives.
The covariance function is given by
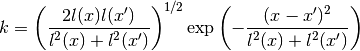
Warps the length scale using a “bucket” function with quintic joins.
The order of the hyperparameters is:
0 sigmaf Amplitude of the covariance function 1 l1 Length scale to the left of the bucket. 2 l2 Length scale in the bucket. 3 l3 Length scale to the right of the bucket. 4 x0 Location of the center of the bucket. 5 w1 Width of the left side quintic section. 6 w2 Width of the bucket. 7 w3 Width of the right side quintic section. Parameters: **kwargs
All parameters are passed to
Kernel.
-
gptools.kernel.gibbs.exp_gauss_warp(X, n, l0, *msb)[source]¶ Length scale function which is an exponential of a sum of Gaussians.
The centers and widths of the Gaussians are free parameters.
The length scale function is given by
rac{(x-mu_i)^2}{2sigma_i^2} ight ) ight )
The number of parameters is equal to the three times the number of Gaussians plus 1 (for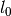 ). This function is inspired by what Gibbs used in
his PhD thesis.
). This function is inspired by what Gibbs used in
his PhD thesis.Parameters: X : 1d or 2d array of float
The points to evaluate the function at. If 2d, it should only have one column (but this is not checked to save time).
- n : int
The derivative order to compute. Used for all X.
- l0 : float
The covariance length scale at the edges of the domain.
- *msb : floats
Means, standard deviations and weights for each Gaussian, in that order.
-
class
gptools.kernel.gibbs.GibbsKernel1dExpGauss(n_gaussians, **kwargs)[source]¶ Bases:
gptools.kernel.gibbs.GibbsKernel1dGibbs warped squared exponential covariance function in 1d.
Uses hard-coded implementation up to first derivatives.
The covariance function is given by
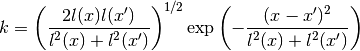
Warps the length scale using an exponential of Gaussian basis functions.
The order of the hyperparameters is:
0 sigmaf Amplitude of the covariance function. 1 l0 Length far away from the Gaussians. 2 mu1 Mean of first Gaussian. 3 mu2 And so on for all Gaussians... 4 sigma1 Width of first Gaussian. 5 sigma2 And so on for all Gaussians... 6 beta1 Amplitude of first Gaussian. 7 beta2 And so on for all Gaussians... Parameters: n_gaussians : int
The number of Gaussian basis functions to use.
**kwargs
All keywords are passed to
Kernel.
-
class
gptools.kernel.gibbs.BSplineWarp(k=3)[source]¶ Bases:
objectLength scale function which is a B-spline.
The degree is fixed at creation, the knot locations and coefficients are free parameters.
Parameters: k : int, optional
The polynomial degree to use. Default is 3 (cubic).
-
__call__(X, n, *tC)[source]¶ Evaluate the length scale function with the given knots and coefficients.
If X is 2d, uses the first column.
Parameters: X : array of float, (N,)
The points to evaluate the length scale function at.
n : int
The derivative order to compute.
*tC : 2M + k - 1 floats
The M knots followed by the M + k - 1 coefficients to use.
-
-
class
gptools.kernel.gibbs.GibbsKernel1dBSpline(nt, k=3, **kwargs)[source]¶ Bases:
gptools.kernel.gibbs.GibbsKernel1dGibbs warped squared exponential covariance function in 1d.
Uses hard-coded implementation up to first derivatives.
The covariance function is given by
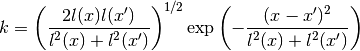
Warps the length scale using a B-spline with free knots but fixed order.
You should always put fixed boundary knots at or beyond the edge of your domain, otherwise the length scale will go to zero. You should always use hyperpriors which keep the coefficients positive, otherwise the length scale can go to zero/be negative.
The order of the hyperparameters is:
0 sigmaf Amplitude of the covariance function. 1 t1 First knot locations. 2 t2 And so on for all nt knots... 3 C1 First coefficient. 4 C2 And so on for all nt + k - 1 coefficients... Parameters: nt : int
Number of knots to use. Should be at least two (at the edges of the domain of interest).
k : int, optional
The polynomial degree to use. Default is 3 (cubic).
**kwargs
All keywords are passed to
Kernel.
-
class
gptools.kernel.gibbs.GPWarp(npts, k=None)[source]¶ Bases:
objectLength scale function which is a Gaussian process.
Parameters: npts : int
The number of points the GP’s value will be specified on.
k :
Kernelinstance, optionalThe covariance kernel to use for the GP. The default is to use a
SquaredExponentialKernelwith fixed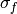 (since it does not matter here) and broad
bounds on
(since it does not matter here) and broad
bounds on 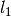 .
.
-
class
gptools.kernel.gibbs.GibbsKernel1dGP(npts, k=None, **kwargs)[source]¶ Bases:
gptools.kernel.gibbs.GibbsKernel1dGibbs warped squared exponential covariance function in 1d.
Uses hard-coded implementation up to first derivatives.
The covariance function is given by
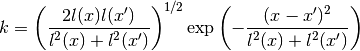
Warps the length scale using a Gaussian process which interpolates the values specified at a set number of points. Both the values and the locations of the points can be treated as free parameters.
You should try to pick a hyperprior which keeps the outer points close to the edge of the domain, as otherwise the Gaussian process will try to go to zero there. You should put a hyperprior on the values at the points which keeps them positive, otherwise unphysical length scales will result.
The order of the hyperparameters is:
0 sigmaf Amplitude of the covariance function. 1 hp1 First hyperparameter of the covariance function. 2 hp2 And so on for all free hyperparameters... 3 x1 Location of the first point to set the value at. 4 x2 And so on for all points the value is set at... 5 y1 Length scale at the first point. 6 y2 And so on for all points the value is set at... Parameters: npts : int
Number of points to use.
k :
Kernelinstance, optionalThe covariance kernel to use for the GP. The default is to use a
SquaredExponentialKernelwith fixed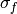 (since it does not matter here) and broad
bounds on
(since it does not matter here) and broad
bounds on 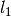 .
.**kwargs
All keywords are passed to
Kernel.
gptools.kernel.matern module¶
Provides the MaternKernel class which implements the anisotropic Matern kernel.
-
gptools.kernel.matern.matern_function(Xi, Xj, *args)[source]¶ Matern covariance function of arbitrary dimension, for use with
ArbitraryKernel.The Matern kernel has the following hyperparameters, always referenced in the order listed:
0 sigma prefactor 1 nu order of kernel 2 l1 length scale for the first dimension 3 l2 ...and so on for all dimensions The kernel is defined as:
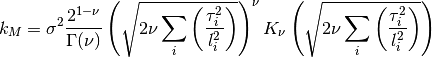
Parameters: Xi, Xj :
Array,mpf, tuple or scalar floatPoints to evaluate the covariance between. If they are
Array,scipyfunctions are used, otherwisempmathfunctions are used.*args
Remaining arguments are the 2+num_dim hyperparameters as defined above.
-
class
gptools.kernel.matern.MaternKernelArb(**kwargs)[source]¶ Bases:
gptools.kernel.core.ArbitraryKernelMatern covariance kernel. Supports arbitrary derivatives. Treats order as a hyperparameter.
This version of the Matern kernel is painfully slow, but uses
mpmathto ensure the derivatives are computed properly, since there may be issues with the regularMaternKernel.The Matern kernel has the following hyperparameters, always referenced in the order listed:
0 sigma prefactor 1 nu order of kernel 2 l1 length scale for the first dimension 3 l2 ...and so on for all dimensions The kernel is defined as:
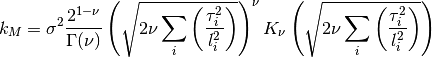
Parameters: **kwargs
All keyword parameters are passed to
ArbitraryKernel.-
nu¶ Returns the value of the order
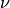 .
.
-
-
class
gptools.kernel.matern.MaternKernel1d(**kwargs)[source]¶ Bases:
gptools.kernel.core.KernelMatern covariance kernel. Only for univariate data. Only supports up to first derivatives. Treats order as a hyperparameter.
The Matern kernel has the following hyperparameters, always referenced in the order listed:
0 sigma prefactor 1 nu order of kernel 2 l1 length scale The kernel is defined as:
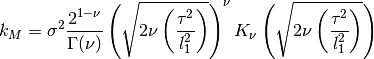
where
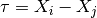 .
.Note that the expressions for the derivatives break down for
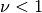 .
.Parameters: **kwargs
All keyword parameters are passed to
Kernel.-
__call__(Xi, Xj, ni, nj, hyper_deriv=None, symmetric=False)[source]¶ Evaluate the covariance between points Xi and Xj with derivative order ni, nj.
Parameters: Xi :
Matrixor other Array-like, (M, D)M inputs with dimension D.
Xj :
Matrixor other Array-like, (M, D)M inputs with dimension D.
ni :
Matrixor other Array-like, (M, D)M derivative orders for set i.
nj :
Matrixor other Array-like, (M, D)M derivative orders for set j.
hyper_deriv : Non-negative int or None, optional
The index of the hyperparameter to compute the first derivative with respect to. If None, no derivatives are taken. Hyperparameter derivatives are not supported at this point. Default is None.
symmetric : bool, optional
Whether or not the input Xi, Xj are from a symmetric matrix. Default is False.
Returns: Kij :
Array, (M,)Covariances for each of the M Xi, Xj pairs.
Raises: NotImplementedError
If the hyper_deriv keyword is not None.
-
-
class
gptools.kernel.matern.MaternKernel(num_dim=1, **kwargs)[source]¶ Bases:
gptools.kernel.core.ChainRuleKernelMatern covariance kernel. Supports arbitrary derivatives. Treats order as a hyperparameter.
The Matern kernel has the following hyperparameters, always referenced in the order listed:
0 sigma prefactor 1 nu order of kernel 2 l1 length scale for the first dimension 3 l2 ...and so on for all dimensions The kernel is defined as:
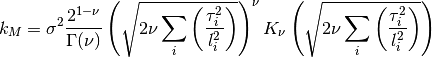
Parameters: num_dim : int
Number of dimensions of the input data. Must be consistent with the X and Xstar values passed to the
GaussianProcessyou wish to use the covariance kernel with.**kwargs
All keyword parameters are passed to
ChainRuleKernel.Raises: ValueError
If num_dim is not a positive integer or the lengths of the input vectors are inconsistent.
GPArgumentError
If fixed_params is passed but initial_params is not.
-
nu¶ Returns the value of the order
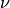 .
.
-
-
class
gptools.kernel.matern.Matern52Kernel(num_dim=1, **kwargs)[source]¶ Bases:
gptools.kernel.core.KernelMatern 5/2 covariance kernel. Supports only 0th and 1st derivatives and is fixed at nu=5/2. Because of these limitations, it is quite a bit faster than the more general Matern kernels.
The Matern52 kernel has the following hyperparameters, always referenced in the order listed:
0 sigma prefactor 1 l1 length scale for the first dimension 2 l2 ...and so on for all dimensions The kernel is defined as:
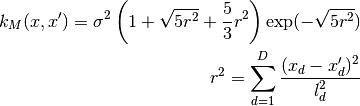
Parameters: num_dim : int
Number of dimensions of the input data. Must be consistent with the X and Xstar values passed to the
GaussianProcessyou wish to use the covariance kernel with.**kwargs
All keyword parameters are passed to
Kernel.Raises: ValueError
If num_dim is not a positive integer or the lengths of the input vectors are inconsistent.
GPArgumentError
If fixed_params is passed but initial_params is not.
-
__call__(Xi, Xj, ni, nj, hyper_deriv=None, symmetric=False)[source]¶ Evaluate the covariance between points Xi and Xj with derivative order ni, nj.
Parameters: Xi :
Matrixor other Array-like, (M, D)M inputs with dimension D.
Xj :
Matrixor other Array-like, (M, D)M inputs with dimension D.
ni :
Matrixor other Array-like, (M, D)M derivative orders for set i.
nj :
Matrixor other Array-like, (M, D)M derivative orders for set j.
hyper_deriv : Non-negative int or None, optional
The index of the hyperparameter to compute the first derivative with respect to. If None, no derivatives are taken. Hyperparameter derivatives are not supported at this point. Default is None.
symmetric : bool
Whether or not the input Xi, Xj are from a symmetric matrix. Default is False.
Returns: Kij :
Array, (M,)Covariances for each of the M Xi, Xj pairs.
Raises: NotImplementedError
If the hyper_deriv keyword is not None.
-
gptools.kernel.noise module¶
Provides classes for implementing uncorrelated noise.
-
class
gptools.kernel.noise.DiagonalNoiseKernel(num_dim=1, initial_noise=None, fixed_noise=False, noise_bound=None, n=0, hyperprior=None)[source]¶ Bases:
gptools.kernel.core.KernelKernel that has constant, independent noise (i.e., a diagonal kernel).
Parameters: num_dim : positive int
Number of dimensions of the input data.
initial_noise : float, optional
Initial value for the noise standard deviation. Default value is None (noise gets set to 1).
fixed_noise : bool, optional
Whether or not the noise is taken to be fixed when optimizing the log likelihood. Default is False (noise is not fixed).
noise_bound : 2-tuple, optional
The bounds for the noise when optimizing the log likelihood with
scipy.optimize.minimize(). Must be of the form (lower, upper). Set a given entry to None to put no bound on that side. Default is None, which gets set to (0, None).n : non-negative int or tuple of non-negative ints with length equal to num_dim, optional
Indicates which derivative this noise is with respect to. Default is 0 (noise applies to value).
hyperprior : callable, optional
Function that returns the prior log-density for a possible value of noise when called. Must also have an attribute called
boundsthat is the bounds on the noise and a method calledrandom_draw()that yields a random draw. Default behavior is to assign a uniform prior.-
__call__(Xi, Xj, ni, nj, hyper_deriv=None, symmetric=False)[source]¶ Evaluate the covariance between points Xi and Xj with derivative order ni, nj.
Parameters: Xi :
Matrixor other Array-like, (M, D)M inputs with dimension D.
Xj :
Matrixor other Array-like, (M, D)M inputs with dimension D.
ni :
Matrixor other Array-like, (M, D)M derivative orders for set i.
nj :
Matrixor other Array-like, (M, D)M derivative orders for set j.
hyper_deriv : Non-negative int or None, optional
The index of the hyperparameter to compute the first derivative with respect to. Since this kernel only has one hyperparameter, 0 is the only valid value. If None, no derivatives are taken. Default is None (no hyperparameter derivatives).
symmetric : bool, optional
Whether or not the input Xi, Xj are from a symmetric matrix. Default is False.
Returns: Kij :
Array, (M,)Covariances for each of the M Xi, Xj pairs.
-
-
class
gptools.kernel.noise.ZeroKernel(num_dim=1)[source]¶ Bases:
gptools.kernel.noise.DiagonalNoiseKernelKernel that always evaluates to zero, used as the default noise kernel.
Parameters: num_dim : positive int
The number of dimensions of the inputs.
-
__call__(Xi, Xj, ni, nj, hyper_deriv=None, symmetric=False)[source]¶ Return zeros the same length as the input Xi.
Ignores all other arguments.
Parameters: Xi :
Matrixor other Array-like, (M, D)M inputs with dimension D.
Xj :
Matrixor other Array-like, (M, D)M inputs with dimension D.
ni :
Matrixor other Array-like, (M, D)M derivative orders for set i.
nj :
Matrixor other Array-like, (M, D)M derivative orders for set j.
hyper_deriv : Non-negative int or None, optional
The index of the hyperparameter to compute the first derivative with respect to. Since this kernel only has one hyperparameter, 0 is the only valid value. If None, no derivatives are taken. Default is None (no hyperparameter derivatives).
symmetric : bool, optional
Whether or not the input Xi, Xj are from a symmetric matrix. Default is False.
Returns: Kij :
Array, (M,)Covariances for each of the M Xi, Xj pairs.
-
gptools.kernel.rational_quadratic module¶
Provides the RationalQuadraticKernel class which implements the anisotropic rational quadratic (RQ) kernel.
-
class
gptools.kernel.rational_quadratic.RationalQuadraticKernel(num_dim=1, **kwargs)[source]¶ Bases:
gptools.kernel.core.ChainRuleKernelRational quadratic (RQ) covariance kernel. Supports arbitrary derivatives.
The RQ kernel has the following hyperparameters, always referenced in the order listed:
0 sigma prefactor. 1 alpha order of kernel. 2 l1 length scale for the first dimension. 3 l2 ...and so on for all dimensions. The kernel is defined as:
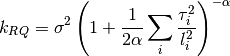
Parameters: num_dim : int
Number of dimensions of the input data. Must be consistent with the X and Xstar values passed to the
GaussianProcessyou wish to use the covariance kernel with.**kwargs
All keyword parameters are passed to
ChainRuleKernel.Raises: ValueError
If num_dim is not a positive integer or the lengths of the input vectors are inconsistent.
GPArgumentError
If fixed_params is passed but initial_params is not.
gptools.kernel.squared_exponential module¶
Provides the SquaredExponentialKernel class that implements the anisotropic SE kernel.
-
class
gptools.kernel.squared_exponential.SquaredExponentialKernel(num_dim=1, **kwargs)[source]¶ Bases:
gptools.kernel.core.KernelSquared exponential covariance kernel. Supports arbitrary derivatives.
Supports derivatives with respect to the hyperparameters.
The squared exponential has the following hyperparameters, always referenced in the order listed:
0 sigma prefactor on the SE 1 l1 length scale for the first dimension 2 l2 ...and so on for all dimensions The kernel is defined as:
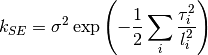
Parameters: num_dim : int
Number of dimensions of the input data. Must be consistent with the X and Xstar values passed to the
GaussianProcessyou wish to use the covariance kernel with.**kwargs
All keyword parameters are passed to
Kernel.Raises: ValueError
If num_dim is not a positive integer or the lengths of the input vectors are inconsistent.
GPArgumentError
If fixed_params is passed but initial_params is not.
-
__call__(Xi, Xj, ni, nj, hyper_deriv=None, symmetric=False)[source]¶ Evaluate the covariance between points Xi and Xj with derivative order ni, nj.
Parameters: Xi :
Matrixor other Array-like, (M, D)M inputs with dimension D.
Xj :
Matrixor other Array-like, (M, D)M inputs with dimension D.
ni :
Matrixor other Array-like, (M, D)M derivative orders for set i.
nj :
Matrixor other Array-like, (M, D)M derivative orders for set j.
hyper_deriv : Non-negative int or None, optional
The index of the hyperparameter to compute the first derivative with respect to. If None, no derivatives are taken. Default is None (no hyperparameter derivatives). Hyperparameter derivatives are not support for n > 0 at this time.
symmetric : bool, optional
Whether or not the input Xi, Xj are from a symmetric matrix. Default is False.
Returns: Kij :
Array, (M,)Covariances for each of the M Xi, Xj pairs.
-
gptools.kernel.warping module¶
Classes and functions to warp inputs to kernels to enable fitting of nonstationary data. Note that this accomplishes a similar goal as the Gibbs kernel (which is a nonstationary version of the squared exponential kernel), but with the difference that the warpings in this module can be applied to any existing kernel. Furthermore, whereas the Gibbs kernel implements nonstationarity by changing the length scale of the covariance function, the warpings in the module act by transforming the input values directly.
The module contains two core classes that work together.
WarpingFunction gives you a way to wrap a given function in a way
that allows you to optimize/integrate over the hyperparameters that describe the
warping. WarpedKernel is an extension of the Kernel base
class and is how you apply a WarpingFunction to whatever kernel you
want to warp.
Two useful warpings have been implemented at this point:
BetaWarpedKernel warps the inputs using the CDF of the beta
distribution (i.e., the regularized incomplete beta function). This requires
that the starting inputs be constrained to the unit hypercube [0, 1]. In order
to get arbitrary data to this form, LinearWarpedKernel allows you to
apply a linear transformation based on the known bounds of your data.
So, for example, to make a beta-warped squared exponential kernel, you simply type:
k_SE = gptools.SquaredExponentialKernel()
k_SE_beta = gptools.BetaWarpedKernel(k_SE)
Furthermore, if your inputs X are not confined to the unit hypercube [0, 1], you should use a linear transformation to map them to it:
k_SE_beta_unit = gptools.LinearWarpedKernel(k_SE_beta, X.min(axis=0), X.max(axis=0))
-
class
gptools.kernel.warping.WarpingFunction(fun, num_dim=1, num_params=None, initial_params=None, fixed_params=None, param_bounds=None, param_names=None, enforce_bounds=False, hyperprior=None)[source]¶ Bases:
objectWrapper to interface a function with
WarpedKernel.This lets you define a simple function fun(X, d, n, p1, p2, ...) that operates on one dimension of X at a time and has several hyperparameters.
Parameters: fun : callable
Must have fingerprint fun(X, d, n, p1, p2, ...) where X is an array of length M, d is the index of the dimension X is from, n is a non-negative integer representing the order of derivative to take and p1, p2, ... are the parameters of the warping. Note that this form assumes that the warping is applied independently to each dimension.
num_dim : positive int, optional
Number of dimensions of the input data. Must be consistent with the X and Xstar values passed to the
GaussianProcessyou wish to use the warping function with. Default is 1.num_params : Non-negative int, optional
Number of parameters in the model. Default is to determine the number of parameters by inspection of fun or the other arguments provided.
initial_params : Array, (num_params,), optional
Initial values to set for the hyperparameters. Default is None, in which case 1 is used for the initial values.
fixed_params : Array of bool, (num_params,), optional
Sets which hyperparameters are considered fixed when optimizing the log likelihood. A True entry corresponds to that element being fixed (where the element ordering is as defined in the class). Default value is None (no hyperparameters are fixed).
param_bounds : list of 2-tuples (num_params,), optional
List of bounds for each of the hyperparameters. Each 2-tuple is of the form (lower`, upper). If there is no bound in a given direction, it works best to set it to something big like 1e16. Default is (0.0, 1e16) for each hyperparameter. Note that this is overridden by the hyperprior keyword, if present.
param_names : list of str (num_params,), optional
List of labels for the hyperparameters. Default is all empty strings.
enforce_bounds : bool, optional
If True, an attempt to set a hyperparameter outside of its bounds will result in the hyperparameter being set right at its bound. If False, bounds are not enforced inside the kernel. Default is False (do not enforce bounds).
hyperprior :
JointPriorinstance or list, optionalJoint prior distribution for all hyperparameters. Can either be given as a
JointPriorinstance or a list of num_params callables orrv_frozeninstances fromscipy.stats, in which case aIndependentJointPrioris constructed with these as the independent priors on each hyperparameter. Default is a uniform PDF on all hyperparameters.-
__call__(X, d, n)[source]¶ Evaluate the warping function.
Parameters: X : Array, (M,)
M inputs corresponding to dimension d.
d : non-negative int
Index of the dimension that X is from.
n : non-negative int
Derivative order to compute.
-
param_bounds¶
-
set_hyperparams(new_params)[source]¶ Sets the free hyperparameters to the new parameter values in new_params.
Parameters: new_params :
Arrayor other Array-like, (len(self.params),)New parameter values, ordered as dictated by the docstring for the class.
-
num_free_params¶ Returns the number of free parameters.
-
free_param_idxs¶ Returns the indices of the free parameters in the main arrays of parameters, etc.
-
free_params¶ Returns the values of the free hyperparameters.
Returns: free_params :
ArrayArray of the free parameters, in order.
-
free_param_bounds¶ Returns the bounds of the free hyperparameters.
Returns: free_param_bounds :
ArrayArray of the bounds of the free parameters, in order.
-
free_param_names¶ Returns the names of the free hyperparameters.
Returns: free_param_names :
ArrayArray of the names of the free parameters, in order.
-
-
gptools.kernel.warping.beta_cdf_warp(X, d, n, *args)[source]¶ Warp inputs that are confined to the unit hypercube using the regularized incomplete beta function.
Applies separately to each dimension, designed for use with
WarpingFunction.Assumes that your inputs X lie entirely within the unit hypercube [0, 1].
Note that you may experience some issues with constraining and computing derivatives at
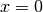 when
when 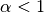 and at
and at 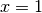 when
when
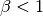 . As a workaround, try mapping your data to not touch the
boundaries of the unit hypercube.
. As a workaround, try mapping your data to not touch the
boundaries of the unit hypercube.Parameters: X : array, (M,)
M inputs from dimension d.
d : non-negative int
The index (starting from zero) of the dimension to apply the warping to.
n : non-negative int
The derivative order to compute.
*args : 2N scalars
The remaining parameters to describe the warping, given as scalars. These are given as alpha_i, beta_i for each of the D dimensions. Note that these must ALL be provided for each call.
References
[R1] J. Snoek, K. Swersky, R. Zemel, R. P. Adams, “Input Warping for Bayesian Optimization of Non-stationary Functions” ICML (2014)
-
gptools.kernel.warping.linear_warp(X, d, n, *args)[source]¶ Warp inputs with a linear transformation.
Applies the warping
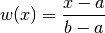
to each dimension. If you set a=min(X) and b=max(X) then this is a convenient way to map your inputs to the unit hypercube.
Parameters: X : array, (M,)
M inputs from dimension d.
d : non-negative int
The index (starting from zero) of the dimension to apply the warping to.
n : non-negative int
The derivative order to compute.
*args : 2N scalars
The remaining parameters to describe the warping, given as scalars. These are given as a_i, b_i for each of the D dimensions. Note that these must ALL be provided for each call.
-
class
gptools.kernel.warping.ISplineWarp(nt, k=3)[source]¶ Bases:
objectWarps inputs with an I-spline.
Applies the warping
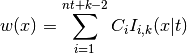
to each dimension, where
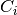 are the coefficients and
are the coefficients and
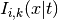 are the I-spline basis functions with knot grid
are the I-spline basis functions with knot grid
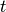 .
.Parameters: nt : int or array of int (D,)
The number of knots. If this is a single int, it is used for all of the dimensions. If it is an array of ints, it is the number of knots for each dimension.
k : int, optional
The polynomial degree of I-spline to use. The same degree is used for all dimensions. The default is 3 (cubic I-splines).
-
__call__(X, d, n, *args)[source]¶ Evaluate the I-spline warping function.
Parameters: X : array, (M,)
M inputs from dimension d.
d : non-negative int
The index (starting from zero) of the dimension to apply the warping to.
n : non-negative int
The derivative order to compute.
*args : scalar flots
The remaining parameters to describe the warping, given as scalars. These are given as the knots followed by the coefficients, for each dimension. Note that these must ALL be provided for each call.
-
-
class
gptools.kernel.warping.WarpedKernel(k, w)[source]¶ Bases:
gptools.kernel.core.KernelKernel which has had its inputs warped through a basic, elementwise warping function.
In other words, takes
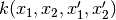 and turns it into
and turns it into
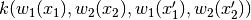 .
.-
w_func(X, d, n)[source]¶ Evaluate the (possibly recursive) warping function and its derivatives.
Parameters: X : array, (M,)
The points (from dimension d) to evaluate the warping function at.
d : int
The dimension to warp.
n : int
The derivative order to compute. So far only 0 and 1 are supported.
-
enforce_bounds¶ Boolean indicating whether or not the kernel will explicitly enforce the bounds defined by the hyperprior.
-
fixed_params¶
-
params¶
-
param_names¶
-
free_params¶
-
free_param_bounds¶
-
free_param_names¶
-
-
class
gptools.kernel.warping.BetaWarpedKernel(k, **w_kwargs)[source]¶ Bases:
gptools.kernel.warping.WarpedKernelClass to warp any existing
Kernelwith the beta CDF.Assumes that your inputs X lie entirely within the unit hypercube [0, 1].
Note that you may experience some issues with constraining and computing derivatives at
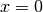 when
when 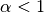 and at
and at 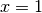 when
when
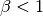 . As a workaround, try mapping your data to not touch the
boundaries of the unit hypercube.
. As a workaround, try mapping your data to not touch the
boundaries of the unit hypercube.Parameters: k :
KernelThe
Kernelto warp.**w_kwargs : optional kwargs
All additional kwargs are passed to the constructor of
WarpingFunction. If no hyperprior or param_bounds are provided, takes each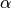 ,
, 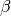 to follow the
log-normal distribution.
to follow the
log-normal distribution.References
[R2] J. Snoek, K. Swersky, R. Zemel, R. P. Adams, “Input Warping for Bayesian Optimization of Non-stationary Functions” ICML (2014)
-
class
gptools.kernel.warping.LinearWarpedKernel(k, a, b)[source]¶ Bases:
gptools.kernel.warping.WarpedKernelClass to warp any existing
Kernelwith the linear transformation given inlinear_warp().If you set a to be the minimum of your X inputs in each dimension and b to be the maximum then you can use this to map data from an arbitrary domain to the unit hypercube [0, 1], as is required for application of the
BetaWarpedKernel, for instance.Parameters: k :
KernelThe
Kernelto warp.a : list
The a parameter in the linear warping defined in
linear_warp(). This list must have length equal to k.num_dim.b : list
The b parameter in the linear warping defined in
linear_warp(). This list must have length equal to k.num_dim.
-
class
gptools.kernel.warping.ISplineWarpedKernel(k, nt, k_deg=3, **w_kwargs)[source]¶ Bases:
gptools.kernel.warping.WarpedKernelClass to warp any existing
Kernelwith the I-spline transformation given inISplineWarp().Parameters: k :
KernelThe
Kernelto warp.nt : int or array of int
The number of knots. If this is a single int, it is used for all of the dimensions. If it is an array of ints, it is the number of knots for each dimension.
k_deg : int, optional
The polynomial degree of I-spline to use. The same degree is used for all dimensions. The default is 3 (cubic I-splines).
**w_kwargs : optional kwargs
All additional keyword arguments are passed to the constructor of
WarpingFunction.
Module contents¶
Subpackage containing a variety of covariance kernels and associated helpers.